二面角的平面角(二面角的平面角的范围)

数学思想是数学的灵魂，是同学们学习过程中最需要总结的法宝，下面例析数学思想方法在立体几何中的应用。

一. 分类讨论的思想

例1. 不共面的4个定点到平面α的距离都相等，这样的平面α共有。

A. 3个 B. 4个 C. 6个 D. 7个

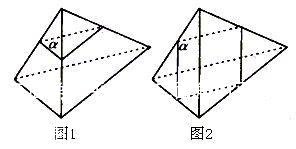
解：把不共面的4个定点看成四面体的4个顶点，平面α可分两类。第一类，如图1所示，4个定点分布在α的一侧1个，另一侧3个，此类α有4个。第二类，如图2所示，4个定点分布在α的两侧各2个，此类α有3个。综上，共有4+3=7（个），故选D。

二. 转化的思想

化归与转化的思想在立体几何中随处可见，特别是空间问题平面化，如空间中的角与距离转化为平面中的角与距离。

例2. 一个与球心距离为1的平面截球所得的截面面积为

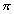
，则球的表面积为

A.

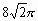
B.

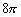
C.

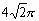
D.

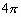
解：如图3所示，作出球的大圆截面图，由截面小圆的面积为

即

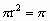
，得

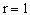
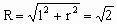
则

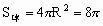
，应选B。

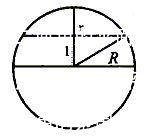
图3

三. 函数的思想

例3. 已知圆锥的底面的半径为R，高为3R，在它的所有内接圆柱中，全面积的最大值是

A.

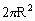
B.

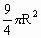
C.

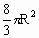
D.

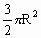
解：如图4所示，设内接圆柱的半径为

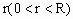
，高为h

则有

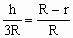
，得

。

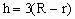
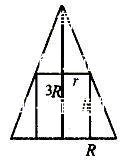
图4

四. 方程的思想

例4. 已知正三棱锥

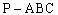
的体积为

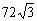
，侧面与底面所成的二面角为60°。

（1）证明：

。

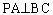
（2）求底面中心O到侧面的距离。

（1）证明：取BC边的中点D

连结AD、PD，则

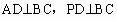
故

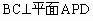
，因此。

（2）解：如图5所示，由（1）可知平面

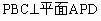
则

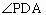
是侧面与底面所成二面角的平面角

由题意知点O到各个侧面的距离相等

过点O作

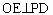
，则OE就是点O到侧面PBC的距离

设

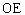
为x，由题意可知点O在AD上

则

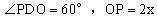
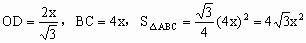
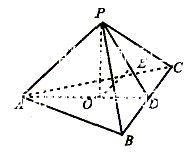
图5

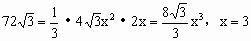
底面中心O到侧面的距离为3。