分数乘分数怎么计算

分数乘分数怎么计算？

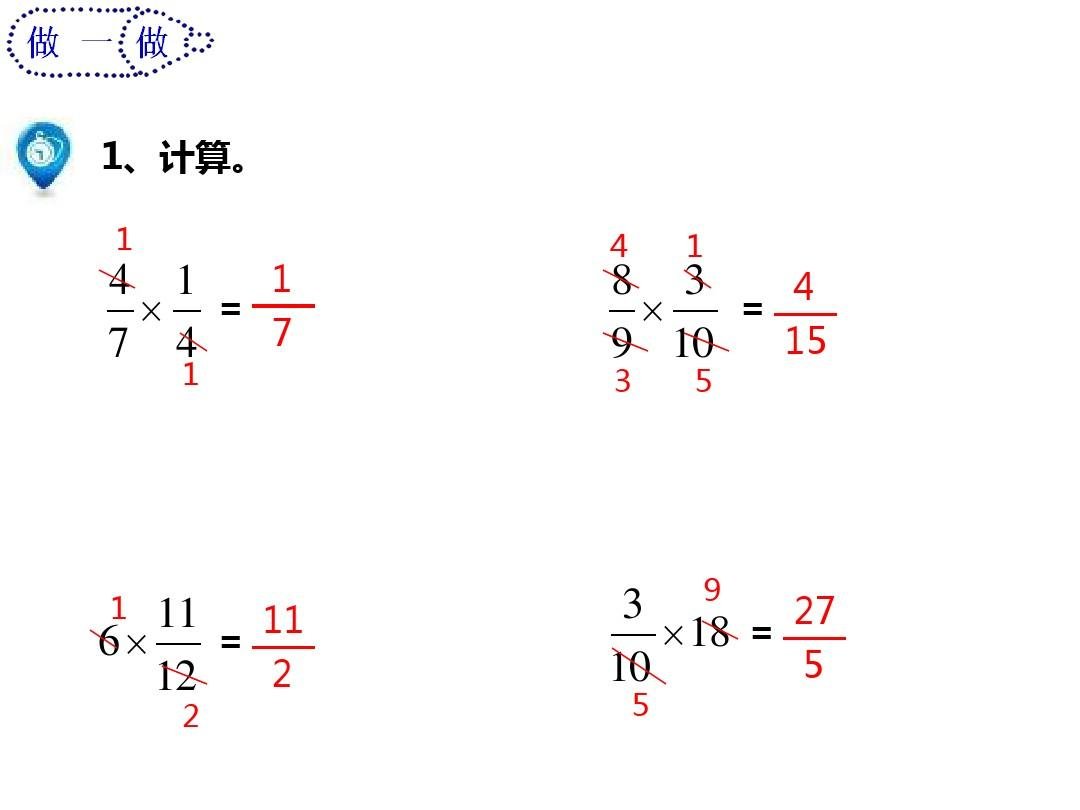
分数乘分数，用分子乘分子，用分母乘分母，最后能约分的要约分。分数乘整数，分母不变，分子乘整数，最后能约分的要约分。最简分数化小数是先看分母的素因数有哪些，如果只有2和5，那么就能化成有限小数，如果不是，就不能化成有限小数，不是最简分数的一定要约分方可判断。分数注意事项：分母一定不能为0，因为分母相当于除数。否则等式无法成立，分子可以等于0，因为分子相当于被除数。相当于0除以任何一个数，不论分母是多少，答案都是0。分数中的分子或分母经过约分后不能出现无理数（如2的平方根），否则就不是分数。一个最简分数的分母中只有2和5两个质因数就能化成有限小数；如果最简分数的分母中只含有2和5以外的质因数那么就能化成纯循环小数；如果最简分数的分母中既含有2或5两个质因数也含有2和5以外的质因数那么就能化成混循环小数。

1.2六年级上册数学《分数乘分数》

参考答案：

一、填空题

1、分数乘分数时，用（分子）相乘的积作（分子），用（分母）相乘的积作（分母）。用字母表示为×=（）。（a,c都不为0).

2、分数乘分数时，能（约分）的先（约分）再计算会更简便。约分时，一般不在（原式）上约分，计算结果一般是（最简分数）。

3、分数和整数相乘时，整数与（分数）的（分母）能约分的直接约分。

4、整数可以看成（分母是1）的分数，所以分数乘整数是分数乘分数的特例。

5、借助直观操作理解分数乘分数地算理，渗透了（数形结合）的数学思想。

6、一个因数（0除外）乘以比1小比0大的数，积（小于）这个因数，若其乘（大于）的数，积大于这个因数，乘以1则（等于）这个因数。

7、公顷的表示（将公顷均分为5份，取其中1份）。

8、一根长千米的丝带，将其均分为5段，其中3段共长（）千米。

9、假设a,b,c是不为0的三个数，a×=b×=c×1，则a,b,c从大到小排序为（b>a>c）。

10、在“（）”里填上“>”“<”或“=”。

（>）××（>）

×（<）×1（=）

二，选择题

11、乘以一个带分数，积（A）.

A、大于

12、把一根木棍截成两段，第一段占全长的，第二段长米，这两段哪段长（A)。

A、第一段长

13、要想×（）的结果是真分数，“（）”里可填（C）。

A、B、C、1

14、一根绳长米，根这样的绳子长（C）米。

15、一个正方形边长为米，其周长和面积各是（B）。

B、m、m2

三、应用题

16、15×=9（吨）9+15=24（吨）

答：仓库里总共24吨大米。

17、45×=5（吨）45-5=40（吨）40-5=35（吨）35÷45==

答：B地原有35吨水泥，原先B地水泥是A地的.

分数乘分数

“分数乘分数，用分子相乘的积做分子，分母相乘的积做分母”这句话相信我们每个成人都会说，也都会用，但我们是否追问过为什么？这样做背后的算理是什么？接下来，再次请出我们的小讲师鲁丹洋为我们分享，分数乘分数的计算算理。

有关分数乘整数的问题，昨天我们已经明白其算理了，今天我将给大家分享分数乘分数的算理。

我们仍然是举例来说明吧，比如1/3×1/5=？我们仍然可以把它转化成小数乘法来计算，但如果数位太大就很麻烦，或者这个分数转换成的小数是无限循环小数怎么办？所以我们还是要探究分数乘分数最简单的方法，它是不是也有自己的运算法则呢？

首先可以用画图的方法，1/3×1/5表示1/3的1/5是多少？也就是将1/3平均分成5份，其中1份占整体的几分之几？画图就是先把一个整体平均分成3份，取其中的1份是1/3。再把其中的1份平均分成5份，取其中的1份。转化成图形语言就是这样的：

最后，我们看一下这其中的1份占整体的几分之几呢？其实就是将原来的3份中的每一份都平均分成5份，也就是15份，那么其中的一份就占整体的1/15。

同样，我还是列了很多分数乘分数的问题，都用画图法来解决。最后，我也发现了一个规律，那便是“分子乘分子，分母乘分母”。但是为什么会是这样的呢？让我们试着在图中找到答案吧。比如2/7×2/3表示把一个整体平均分成7份，取其中的2份，再把这2份平均分成3份，取其中的2份，图形语言是这样的：

我们可以很直观的得到算式的结果是4/21。但这个分数究竟是怎么来的呢？让我们先从分母观察，2/7我们不妨先把它理解为2个1/7。先算1/7×2/3。把整体先平均分成7份，取其中的1份，然后再把这1份平均分成3份，其实也就是将整体平均分成了“3×7”份。因为一共有7大份，每一份又平均分成了3小份，自然就是“3×7”份，这也就是为什么分母乘分母。现在让我们再来看一下分子部分。如果说是1/7×2/3，按照分子乘分子也就是1×2。但这怎么理解呢？原来只有一个分数单位（1/7），怎么一下子就变成了2个分数单位（1/21）了？其实就是因为它把其中一个分数单位平均分成了3份，取了其中的2份。这也就是为什么是分子乘分子。现在算出来的是1/7×2/3，要想计算出2/7×2/3，那么还需要再乘2。（其实在这里也可以说明为什么是分子乘分子，刚刚1/7×2/3的结果从图里可以直观的感受到其结果是2/21，现在要计算2个这样的1/7×2/3，也就是2个2/21，也就是2×2个1/21）

这就是分数乘分数的算理，但是分数乘分数，肯定也会面临着约分的问题，就如同分数乘整数那样。比如，2/3×3/6（亲，3/6是最简分数吗？乘数也必须是最简分数哦，你这个例子举的可不够好呢。）结果是6/18，约分后是1/3。有没有在中间约分的方法呢？肯定是有的，如图：

根据分数基本性质分子分母同时除以一个非零的数，分数大小不变。而这时分子分母正好又有公因数，所以可以直接约分，这样更加的简便。

最后让我们用字母来表示一下分数乘分数的运算法则吧：（亲，a,b,c,d表示的是分子和分母，所以它们还必须是整数哦。）

而分数乘分数与整数乘法有关系，与分数乘整数有关系。因为它们最终都可以转化成分数乘分数。比如，2×3=2/1×3/1=(2×3)/(1×1)=6/1=6，2×2/3=2/1×2/3=(2×2)/(1×3)=4/3。所以最后可以说明，不管是分数乘整数，分数乘分数，还是整数乘法，它们其实最终都是分数乘分数。也就是说，分数乘分数包含了分数乘整数，以及整数乘法。

这便是分数乘法，简单而有趣！你懂分数乘法的算理了吗？

分数乘分数怎么约分

分数乘法的计算结果如果不是不是最简分数，要进行约分，化成最简分数。分数乘分数怎么进行约分呢？下面的经验希望能够帮到你。

方法/步骤

分数乘法的基本法则是：两个分数相乘，分子和分子相乘的积做分子，分母相乘的积做分母。分数乘法中有带分数时，要把带分数化成假分数，然后相乘。如果所得的积不是最简分数，要约成最简分数。为了简便，在计算过程中就要约分。例如：

计算过程中前一个分数的分子和后一个分数的分母如果能约分的就约分，前一个分数的分母与后一个分数的分子能约分的就约分，之后再相乘。这样计算简便。约分的关键是能够很快看出两个数的最大公约数，也需要数的整除性相关知识。例如：

首先看第一个分数的分子和第二个分数的分母，因为个位数都是5，便知道可以用5约分；但是约分后还可以再一次用5约分。能不能一次约分呢，怎么能一下子就看出来呢？因为这两个数的个位数都是5，数的整除性相关知识告诉我们：末位数字是5或0的数能被5整除；只要末两位数字能被25整除的，这个数就能被25整除；只要末三位数字能被125的整除，这个数能被125整除。上题75是25的3倍，可以直接用25约分。这个算式已经变为：

接下来看第一个分数的分母222和后一个分数的分子74。还要应用到数的整除性相关知识：末尾数是偶数的都可以被2整除；111是37的倍数。可以用74约分。全部约分情况和计算结果如下：

希望学习分数的同学一定要复习好数的整除性知识，掌握一些数的特征。比如：

“能被3、9整除的数的特征”：这个数字各个数位上的数字相加之和能被3或9整除。

“能被11整除的数的特征”：隔位数字的和相等或者相减之差能被11整除，这个数就能被11整除。